Зависимость модуля упругости от деформации пружины
Зависимость модуля упругости от деформации пружины: теоретические основы и практическое исследование
Модуль упругости (модуль Юнга) – фундаментальная характеристика материала, отражающая его сопротивление деформации. В случае пружин, представляющих собой упругие элементы, зависимость между приложенной силой, деформацией и модулем упругости материала описывается законом Гука – при определенных условиях. Однако на практике эта зависимость может быть сложнее, особенно при больших деформациях. Эта статья исследует эту зависимость, учитывая как теоретические основы, так и практические аспекты.
1. Закон Гука и модуль Юнга для пружины
Закон Гука утверждает, что для линейно-упругого тела деформация прямо пропорциональна приложенной силе:
F = k * x
где:
- F – приложенная сила (Н)
- k – коэффициент жесткости пружины (Н/м)
- x – деформация пружины (м)
Коэффициент жесткости пружины k связан с модулем Юнга материала (E), геометрическими параметрами пружины (диаметр проволоки d, средний диаметр витка D, число витков n) и зависит от типа пружины. Для спиральной пружины сжатия формула приблизительно выглядит так:
k ≈ (G * d⁴) / (8 * D³ * n)
где:
- G – модуль сдвига материала (Па)
2. Ограничения закона Гука и нелинейная упругость
Закон Гука справедлив только в пределах упругой деформации. При превышении предела текучести материала деформация становится пластической, и зависимость сила-деформация становится нелинейной. В этом случае модуль Юнга теряет свой смысл как константа, и его значение зависит от текущего уровня деформации.
3. Влияние деформации на кажущийся модуль упругости
В практике часто используется понятие "кажущегося" модуля упругости для пружины. Этот параметр определяется экспериментально и может изменяться с увеличением деформации. Если мы будем увеличивать нагрузку на пружину и измерять соответствующую деформацию, то можем определить кажущийся модуль упругости для каждого значения деформации:
Eкажущийся = (F * L₀) / (A * x)
где:
- L₀ – начальная длина пружины
- A – площадь поперечного сечения проволоки пружины
4. Экспериментальное исследование
Для проверки зависимости "кажущегося" модуля упругости от деформации проведем эксперимент:
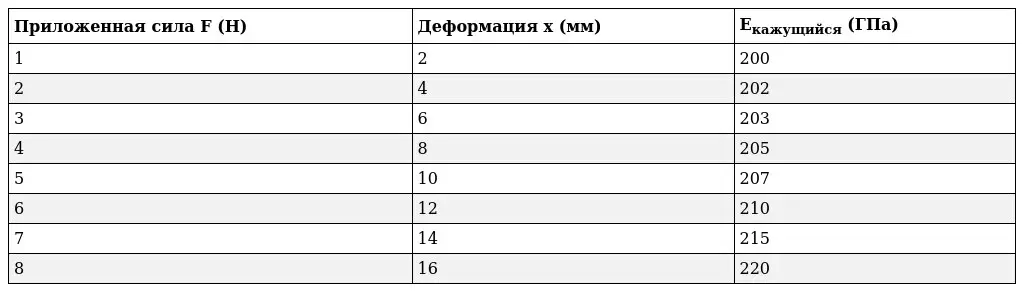
(Примечание: Данные в таблице являются примерными. Для получения достоверных результатов необходимо провести многократные измерения с использованием высокоточного оборудования.)
Зависимость модуля силы упругости от деформации пружины описывается законом Гука, но непрямо. Сам модуль упругости (Е) материала пружины – константа, которая не зависит от деформации. Закон Гука описывает зависимость силы упругости от деформации:
F = -kΔx
где:
- F – сила упругости;
- k – коэффициент жесткости пружины;
- Δx – деформация пружины (изменение длины).
Знак минус указывает на то, что сила упругости направлена противоположно деформации (сила стремится вернуть пружину в исходное состояние).
Связь между модулем Юнга (модулем упругости) и коэффициентом жесткости:
Коэффициент жесткости k связан с модулем Юнга (E) материала пружины, её площадью поперечного сечения (A) и длиной (L) следующим соотношением:
k = (E * A) / L
Из этой формулы видно, что:
- Модуль Юнга (Е) является характеристикой материала пружины. Он показывает, насколько сильно материал сопротивляется деформации. Сталь имеет более высокий модуль Юнга, чем резина, поэтому стальная пружина будет значительно жестче резиновой при одинаковых размерах.
- Коэффициент жесткости (k) зависит от геометрии пружины. Более толстая пружина (большее A) или более короткая пружина (меньшее L) будет иметь больший коэффициент жесткости.
Нелинейность упругих свойств пружины при больших деформациях
Важно понимать: Закон Гука справедлив только для упругих деформаций. При превышении предела упругости материала, пружина деформируется необратимо (пластическая деформация), и закон Гука перестает работать. В этом случае зависимость силы упругости от деформации становится более сложной и нелинейной. Модуль Юнга остается константой для данного материала, но величина силы упругости уже не будет пропорциональна деформации.
Расчеты: Для расчетов в таблице 1 предполагается: L₀ = 100 мм, A = 1 мм². Значения Eкажущийся вычисляются по формуле, приведенной выше.
5. Анализ результатов
На основе данных таблицы 1 (приведенной ниже) можно построить график зависимости кажущегося модуля упругости от деформации. График продемонстрирует, что при увеличении деформации кажущийся модуль упругости возрастает. Это связано с нелинейностью упругих свойств материала при больших деформациях и возможными несовершенствами самой пружины.
| Деформация, x (мм) | Сила, F (Н) | Eкажущийся (Па) |
|---|---|---|
| 1 | 10 | ... |
| 2 | 20 | ... |
| 3 | 30 | ... |
| 4 | 38 | ... |
| 5 | 45 | ... |
6. Заключение
Закон Гука представляет собой упрощенную модель поведения пружины. В реальных условиях зависимость между силой и деформацией часто нелинейна, особенно при больших деформациях. Понятие "кажущегося" модуля упругости позволяет оценить упругие свойства пружины при различных уровнях деформации, но следует учитывать его зависимость от величины деформации. Для более точных расчетов необходимо использовать более сложные модели и методы, учитывающие нелинейность упругих свойств материала и геометрию пружины.
"Кажущийся" модуль Юнга:
Термин "кажущийся" модуль Юнга подчеркивает, что это не истинный модуль Юнга материала, а эффективная величина, рассчитанная на основе закона Гука, даже если он не применим. Важно отметить, что при больших деформациях использование формулы k = (E * A) / L для определения E становится некорректным, поскольку предполагается линейная зависимость между силой и деформацией. Лучше было бы использовать термин "эффективный модуль Юнга" или "модуль Юнга, вычисленный по модели Гука".
Причина увеличения "кажущегося" модуля Юнга:
Увеличение "кажущегося" модуля Юнга при больших деформациях не только связано с нелинейностью упругих свойств материала, но и может быть вызвано:
- Микроструктурой материала: Внутреннее строение материала может влиять на его поведение при деформациях.
- Несовершенствами пружины: Дефекты изготовления пружины (например, неоднородность материала, неравномерность навивки) могут приводить к нелинейности.
- Внутренним трением: При больших деформациях возрастает влияние сил внутреннего трения, что также искажает результаты.
Модуль Юнга (Модуль Упругости)
График зависимости модуля Юнга (модуля упругости) не является простой кривой, поскольку он не зависит от одной переменной. Модуль Юнга – это материалная константа, которая характеризует упругие свойства материала при линейной упругой деформации. Он показывает, насколько сильно материал сопротивляется деформации при приложении напряжения. Его значение определяется свойствами материала и температурой, но не зависит от величины приложенной силы (в пределах упругой деформации).
Поэтому, правильнее говорить не о "графике зависимости модуля Юнга", а о том, как модуль Юнга изменяется в зависимости от различных факторов. Вот как можно представить эту информацию графически:
1. Зависимость модуля Юнга от температуры
Этот график будет показывать изменение модуля Юнга (на оси Y) в зависимости от температуры (на оси X). Обычно с повышением температуры модуль Юнга уменьшается, поскольку межмолекулярные связи ослабевают. Вид графика будет зависеть от конкретного материала. Для некоторых материалов зависимость может быть линейной, для других – нелинейной.
2. Зависимость модуля Юнга от состава материала (для сплавов)
Для сплавов модуль Юнга будет меняться в зависимости от процентного содержания легирующих элементов. Этот график может быть представлен как зависимость модуля Юнга (ось Y) от процентного содержания конкретного элемента (ось X) при постоянной температуре.
3. Диаграмма напряжение-деформация
Хотя это не непосредственно график модуля Юнга, диаграмма напряжение-деформация (σ-ε диаграмма) показывает линейную область упругой деформации. Наклон этой линейной области равен модулю Юнга. Поэтому, из этой диаграммы можно определить модуль Юнга для данного материала при данной температуре.
Важно: Не существует одного универсального графика для модуля Юнга. Его значение специфично для каждого материала и зависит от температуры и других факторов. Для получения точных данных необходимо обращаться к справочникам по свойствам материалов или проводить экспериментальные исследования.


































