Зубчатое зацепление
Зубчатые зацепления: Теория и Расчет
Зубчатые зацепления – это механизмы, передающие вращательный момент между валами с помощью зацепления зубьев. Они широко используются в различных машинах и механизмах благодаря высокой эффективности передачи мощности и компактности. В данной статье рассмотрим основные типы зубчатых зацеплений, их параметры и методы расчета.
1. Типы зубчатых зацеплений:
Зубчатые зацепления классифицируются по различным признакам:
- По форме зубчатых колес: цилиндрические (внешнее и внутреннее зацепление), конические, червячные.
- По виду зацепления: внешнее (зубья заходят друг за друга с внешних сторон), внутреннее (зубья заходят друг за друга с внутренних сторон).
- По форме профиля зуба: эвольвентное (наиболее распространенный тип), циклоидальное, и др.
2. Цилиндрическое зубчатое зацепление:
Наиболее распространенный тип зацепления, характеризующийся параллельными осями вращения зубчатых колес.
2.1. Внешнее цилиндрическое зацепление:
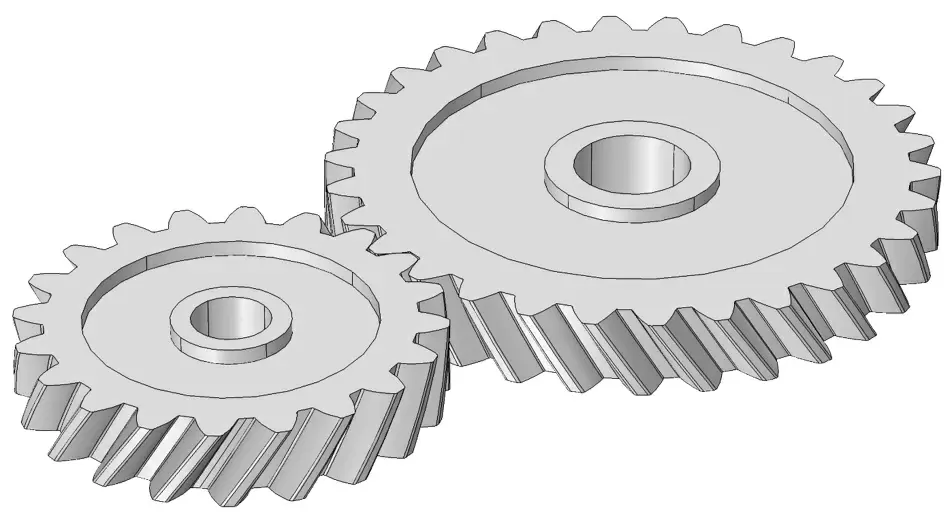
В этом случае зубья взаимодействуют с внешних сторон колес.
2.2. Внутреннее цилиндрическое зацепление:
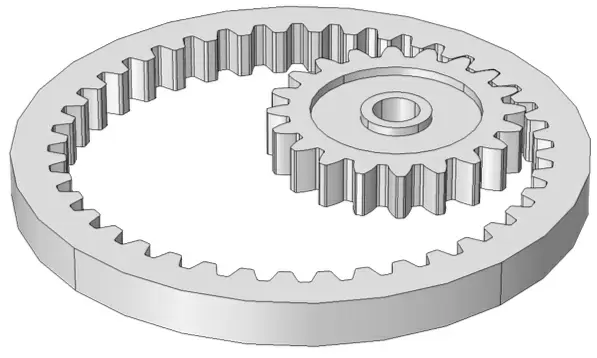
Здесь зубья шестерни зацепляются с внутренними зубьями колеса большего диаметра. Преимущества: компактность, большая передача отношения.
3. Эвольвентное зубчатое зацепление:
Профиль зуба в эвольвентном зацеплении представляет собой эвольвенту окружности. Преимущества: постоянство передаточного отношения, плавность работы, меньшие динамические нагрузки.
4. Параметры зубчатого зацепления:
Основные параметры:
- Модуль (m): основной параметр, определяющий размер зуба. m = d / z, где d - делительный диаметр, z - число зубьев. Единица измерения - мм.
- Делительный диаметр (d): диаметр окружности, по которой происходит зацепление зубьев. d = m * z
- Шаг (p): расстояние между соответствующими точками соседних профилей зубьев по делительной окружности. p = π * m
- Угол зацепления (α): угол между касательной к профилю зуба в точке зацепления и линией центров. Типовое значение: 20°.
- Число зубьев (z): количество зубьев на колесе.
- Межосевое расстояние (a): расстояние между осями вращения колес. a = (d1 + d2) / 2 для внешнего зацепления.
5. Расчет зубчатого зацепления:
Рассмотрим пример расчета параметров цилиндрической зубчатой передачи с внешним зацеплением.
Пример:
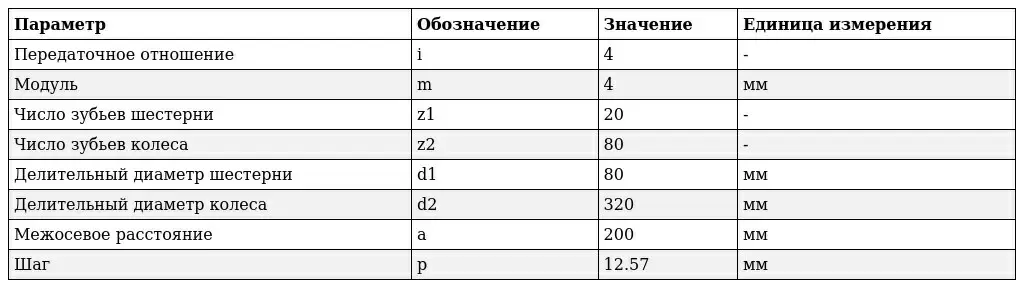
Требуется спроектировать цилиндрическую зубчатую передачу с передаточным отношением i = 4. Модуль m = 4 мм, число зубьев на шестерне z1 = 20.
- Число зубьев на колесе: z2 = z1 * i = 20 * 4 = 80
- Делительные диаметры: d1 = m * z1 = 4 * 20 = 80 мм, d2 = m * z2 = 4 * 80 = 320 мм
- Межосевое расстояние: a = (d1 + d2) / 2 = (80 + 320) / 2 = 200 мм
- Шаг: p = π * m = π * 4 ≈ 12.57 мм
6. Заключение:
Данная статья предоставляет базовые знания о зубчатых зацеплениях. Для более детального проектирования необходимо учитывать дополнительные факторы, такие как: динамические нагрузки, износ, смазка, материалы зубчатых колес, и т.д. Более сложные расчеты требуют применения специализированного программного обеспечения.
Углубленный анализ зубчатых зацеплений
В этой статье мы углубим анализ, рассмотрев дополнительные параметры, формулы и примеры расчета, включая влияние угла зацепления и более сложные аспекты проектирования.
1. Угол зацепления:
Угол зацепления (α) – это угол между касательной к профилю зуба в точке зацепления и линией центров. Стандартный угол зацепления для эвольвентных зубчатых колес составляет 20°, но могут использоваться и другие значения (например, 14.5°, 25°). Выбор угла зацепления влияет на ряд параметров:
- Прочность: больший угол зацепления обычно означает большую контактную жесткость и прочность, но может привести к увеличению боковых сил.
- Износ: оптимальный угол зацепления минимизирует износ зубьев.
- Компактность: меньший угол зацепления позволяет создать более компактные передачи.
Формула для определения длины линии зацепления (L):
L = (m * (z1 + z2) * sin(α)) / (2 * cos(γ))
где:
- m – модуль
- z1, z2 – число зубьев шестерни и колеса соответственно
- α – угол зацепления
- γ – угол спирали (для прямых зубьев γ = 0)
2. Влияние профиля зуба:
Помимо эвольвентного профиля, существуют и другие профили зубьев, например, циклоидальный. Эвольвентный профиль наиболее распространен благодаря своим преимуществам:
- Постоянство передаточного отношения: независимо от положения колес вдоль линии зацепления, передаточное отношение остается постоянным.
- Самоцентрирование: ошибка в межосевом расстоянии не вызывает значительного изменения передаточного отношения.
3. Расчет на прочность:
Прочность зубчатого зацепления определяется по наименьшему напряжению в наиболее нагруженном зубе. Расчет включает в себя определение контактных напряжений и изгибных напряжений. Для упрощенного расчета можно использовать формулу Герца для контактных напряжений:
σ_c = K * √((2 * F * E) / (π * b * L * d_b))
где:
- σ_c – контактное напряжение
- K – коэффициент, учитывающий форму зуба и материал
- F – окружная сила
- E – модуль упругости материала
- b – ширина зуба
- L – длина линии зацепления
- d_b – диаметр базовой окружности
Для изгибных напряжений используются более сложные формулы, часто требующие использования справочных данных и программного обеспечения.
4. Влияние динамических нагрузок:
В реальных условиях на зубчатые колеса действуют динамические нагрузки, вызываемые колебаниями, неравномерностью вращения и другими факторами. Эти нагрузки увеличивают напряжения в зубах и могут привести к преждевременному износу или поломке. Учет динамических нагрузок осуществляется путем введения динамического коэффициента, который увеличивает статическую нагрузку.
5. Расширенный пример расчета:
Рассмотрим передачу с параметрами: m = 5 мм, z1 = 25, z2 = 75, α = 20°, b = 30 мм, F = 1000 Н, E = 210 ГПа, K = 1.5.
- Делительные диаметры: d1 = 5 * 25 = 125 мм, d2 = 5 * 75 = 375 мм
- Межосевое расстояние: a = (125 + 375) / 2 = 250 мм
- Длина линии зацепления (при γ = 0): L = (5 * (25 + 75) * sin(20°)) / (2 * cos(0°)) ≈ 71.7 мм
- Диаметр базовой окружности (d_b = d * cos(α)): d_b1 = 125 * cos(20°) ≈ 117 мм, d_b2 = 375 * cos(20°) ≈ 352 мм. Для расчета возьмем минимальный d_b = d_b1 ≈ 117 мм
- Контактное напряжение (приблизительно): σ_c = 1.5 * √((2 × 1000 × 210e9) / (π × 30 × 71.7 × 117)) ≈ 150 МПа
Этот расчет – упрощенная модель. Для более точного результата необходимо учитывать динамические нагрузки, коэффициенты безопасности и другие факторы.
Шаг и типы зубчатых зацеплений
Рассмотрим более подробно понятие шага в зубчатом зацеплении и различные типы зацеплений, включая их преимущества и недостатки.
1. Шаг в зубчатом зацеплении:
Шаг (p) – это линейное расстояние между соответствующими профилями соседних зубьев, измеренное по делительной окружности. Он тесно связан с модулем (m) и является ключевым параметром, определяющим геометрию зубчатого колеса.
- Прямой шаг (p): Расстояние между одноименными профилями (например, между двумя вершинами или двумя впадинами) соседних зубьев, измеренное вдоль делительной окружности. p = πm (для цилиндрических колес).
- Нормальный шаг (pn): Шаг, проецируемый на плоскость, перпендикулярную к линии зуба. Для цилиндрических колес с прямыми зубьями pn = p. Для конических колес и колес с косыми зубьями pn отличается от p.
- Окружной шаг (pt): Шаг, измеренный по касательной к делительной окружности. Для цилиндрических колес с прямыми зубьями pt = p.
Важно понимать, что шаг – это не просто расстояние между зубьями, а строго определенная величина, определяемая по делительной окружности и связанная с другими параметрами зацепления, такими как модуль и число зубьев. Точность шага критически важна для правильного функционирования передачи. Несоответствие шагов в зацеплении может привести к вибрациям, повышенному износу и поломке.
2. Виды зацеплений:
Помимо уже упомянутых внешнего и внутреннего цилиндрического зацеплений, существуют и другие типы:
a) Цилиндрические зацепления:
- Внешнее зацепление: Зубья шестерни и колеса взаимодействуют с внешних сторон. Наиболее распространенный тип, характеризуется простотой изготовления и надежностью. Передаточное отношение определяется отношением чисел зубьев.
- Внутреннее зацепление: Зубья шестерни зацепляются с внутренними зубьями колеса большего диаметра. Преимущества: компактность (меньшее межосевое расстояние для того же передаточного отношения), большая несущая способность (из-за увеличенной длины линии зацепления). Недостатки: сложность изготовления, повышенные требования к точности.
- Зацепление с косыми зубьями: Зубья имеют наклон относительно оси вращения. Преимущества: более плавная работа, меньший шум, увеличенная несущая способность за счет большей длины линии зацепления. Недостатки: сложность изготовления, появление осевых сил.
- Зацепление с шевронными зубьями: Зубья имеют V-образную форму, образованную двумя косыми зубьями с противоположным наклоном. Преимущества: очень плавная работа, высокая несущая способность, отсутствие осевых сил. Недостатки: сложность изготовления, высокая стоимость.
b) Конические зацепления:
Используются для передачи вращения между валами, пересекающимися под углом. Существуют конические передачи с прямыми, косыми и криволинейными зубьями. Преимущества: компактность, возможность передачи вращения под углом. Недостатки: сложность изготовления, меньшая несущая способность по сравнению с цилиндрическими передачами.
c) Червячные зацепления:
Состоят из червяка (винта) и червячного колеса. Червяк имеет винтовой профиль, который зацепляется с зубьями червячного колеса. Преимущества: большое передаточное отношение, плавность работы, самоторможение (в некоторых случаях). Недостатки: низкий КПД, значительное тепловыделение, сложность изготовления.
d) Планетарные зацепления:
Представляют собой сложную систему, включающую центральное колесо (солнце), сателлиты (малые колеса) и колесо-корона. Преимущества: высокая компактность, возможность получения различных передаточных отношений путем изменения соотношения скоростей вращения элементов. Недостатки: сложность конструкции и регулировки.
3. Выбор типа зацепления:
Выбор типа зацепления зависит от конкретных требований к передаче: передаточное отношение, мощность, скорость, габариты, шум, КПД, стоимость и т.д. Например, для больших передаточных отношений и плавной работы лучше подойдут червячные передачи, а для больших мощностей и высокой скорости – цилиндрические передачи с косыми или шевронными зубьями.
Заключение
Надежная и эффективная работа механизма напрямую зависит от правильного выбора типа зацепления и точности его расчета. Для сложных проектов, требующих высокой точности и учета всех факторов, рекомендуется использовать специализированное программное обеспечение для проектирования зубчатых передач. Это обеспечит оптимальные параметры и продлит срок службы механизма.


































